我们终于要开始介绍B+树和它的基本操作了。这里我们将以 15-445 fall 2020 project2 的实现思路为模板介绍 B+ 树的结构,以图文的形式介绍插入、删除操作以及对应的调整操作,文中不会直接出现代码实现片段;可参照教材「数据库系统概念第六版 - 11.3」中的伪代码。
首先我们明确 B+ 树内部节点和叶节点的结构。
-
内部节点
包含一个 k/v 数组,key 是用于搜索的码值,value 是指向子节点的指针(实现中通常为子节点的page id)。我们通常需要规定一个节点存放元素的上限和下限,若设定上限为 n,则内部节点元素个数的下限为$\lceil \frac{n}{2} \rceil$。当节点已满时,再向其中插入元素就需要对节点进行分裂;若节点因删除而低于下限时,就要进行 distribute 或者 merge 操作来保证元素个数不少于下限。唯一特殊的情况是当根节点是内部节点时,允许它的指针个数少于$\lceil \frac{n}{2} \rceil$,但是至少要包含2个指针(该情况出现在从空树开始构建、根节点作为第一个叶节点溢出分裂后产生一个新的根节点时)。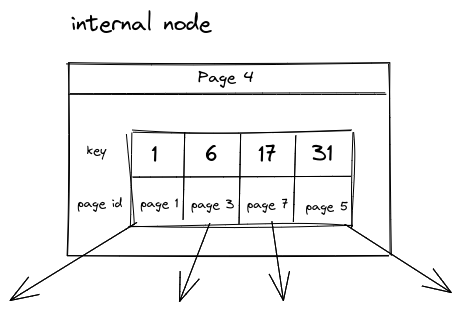
图中第一个 key 的值其实无关紧要,查找时我们是根据第二个 key = 6 得知 page 1 中存放的元素均小于 6。第一个 key 可能是由于内部节点的分裂、合并或重新分配而设置的(即 key=1 原本并不在 index 0 位置上),随着插入和删除操作 key=1 也无法继续代表 page 1 的第一个元素为 1,因此我们可以将内部节点的第一个 key 值当作无意义的(实现上存放和移动该 key 是为了代码逻辑上的统一)。
注意教材中提到典型 B+ 树节点包含 n-1 个 key,以及 n 个指针,其中每个 key 对应一个指针,同时叶节点包含一个指向下一个的 next 指针,用于支持遍历操作。其实我们实现过程中往往创建一个 n-1 长度的 k/v 数组,将 next 指针与 parent 指针单独存放。
-
叶节点
与内部节点类似同样包含一个 k/v 数组,key是用于搜索的码值,value 根据实现方式不同,可以直接存放 tuple 本身(MySQL的实现 // TODO:待考证),也可以存放指向 tuple 实际存放地址的指针,我们这里以后者为例。教材定义叶节点最少包含$\lceil \frac{n-1}{2} \rceil$个元素,最多包含 n - 1 个元素。不过在我看来叶节点的最大元素个数略微超过 n 其实不会造成什么影响,比方说我们定义叶节点的最大元素个数为 n + 1,按照这个标准进行分裂其实也能维持 B+ 树的结构,之所以定义为 n - 1 也许是为了开辟的数组长度与内部节点统一,确实在 C/C++ 中如此操作会比较简便。但在 golang 中如果使用切片之类长度可变的结构存储,那么我们应当可以不受此限制约束(只要能保持树的结构和性质)。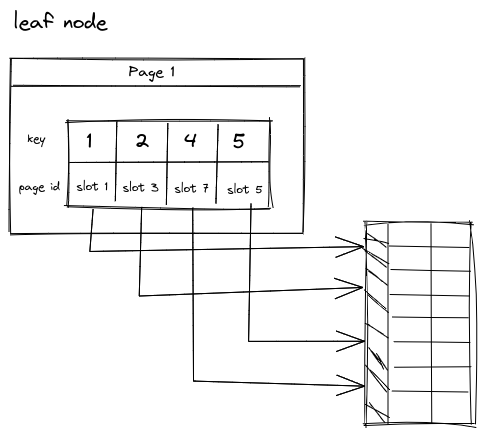
B+ 树的查找过程即与一般二叉搜索树差别不大,从二叉变为多叉树而已,此处不再赘述。主要描述 B+ 树的插入操作和删除操作。
插入
插入操作我们分情况讨论。
- 如果 B+ 树为空,我们首先创建一个叶节点,往里插入第一个值并将其作为根节点
- 如果 B+ 树不为空,那么我们可以查找得到 k/v 应插入的叶节点,此时若:
2.1 叶节点未满,则无需分裂,直接使用二分查找得到应插入的下标,插入 k/v 即可
2.2 若叶节点已满,需要分裂。我们创建一个新的叶节点 new_node,令 new_node 的 parent 指向 old_node 的父节点,更新两个叶节点的 next 指针,将后一半元素拷贝到 new_node 中,最后将 new_node 第一个元素的 key 值插入父节点中相应的位置(保持有序),就完成了叶节点插入的分裂操作。但是由于我们向父节点插入了一个元素,这个操作可能导致父节点也需要进行分裂,因此我们需要不断向上递归直到节点不再进行分裂为止,最坏情况我们会一致递归到根节点并分裂,这样就造成树的高度增加1。中间节点分裂所需操作与叶节点类似,不再重复。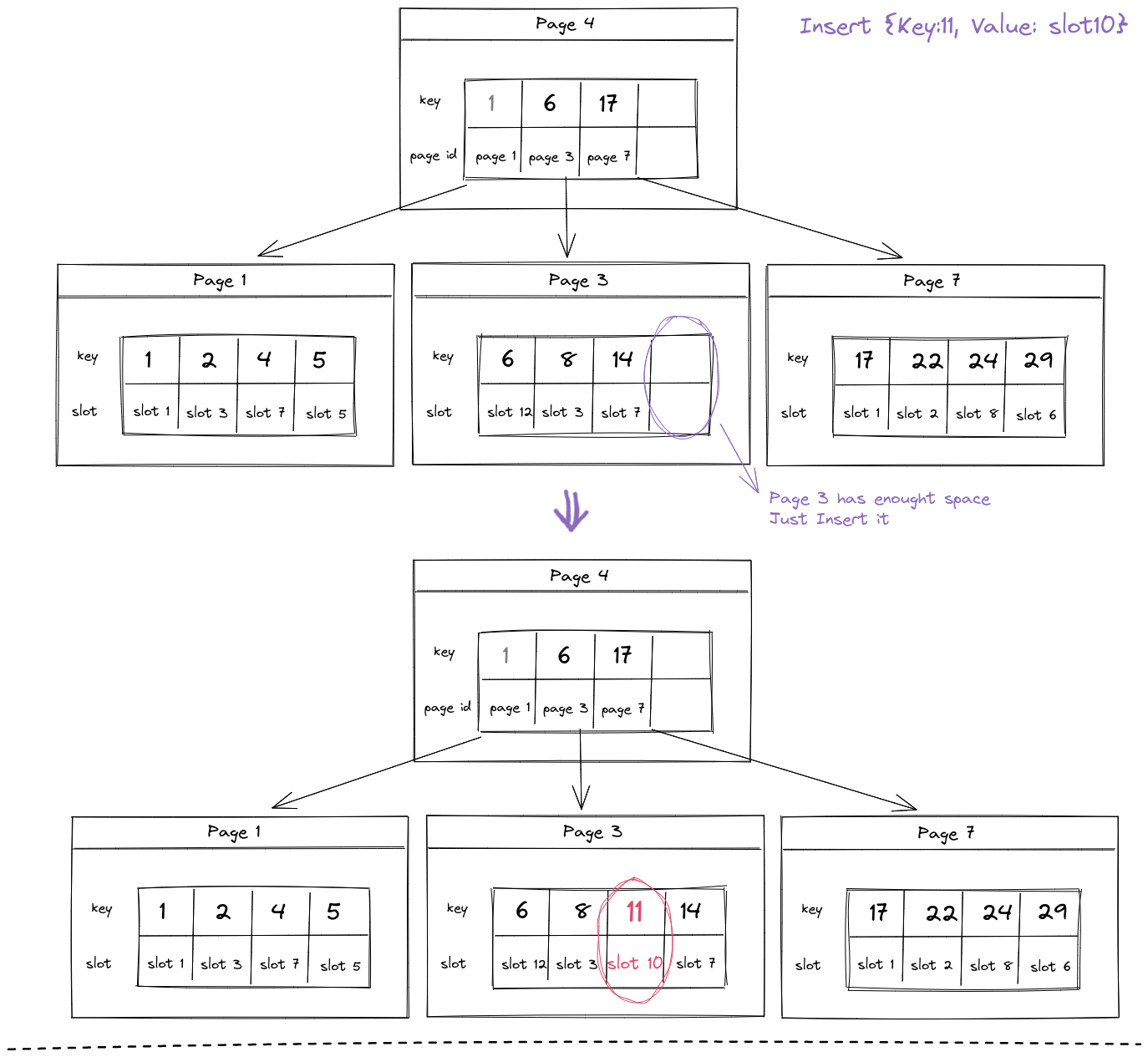
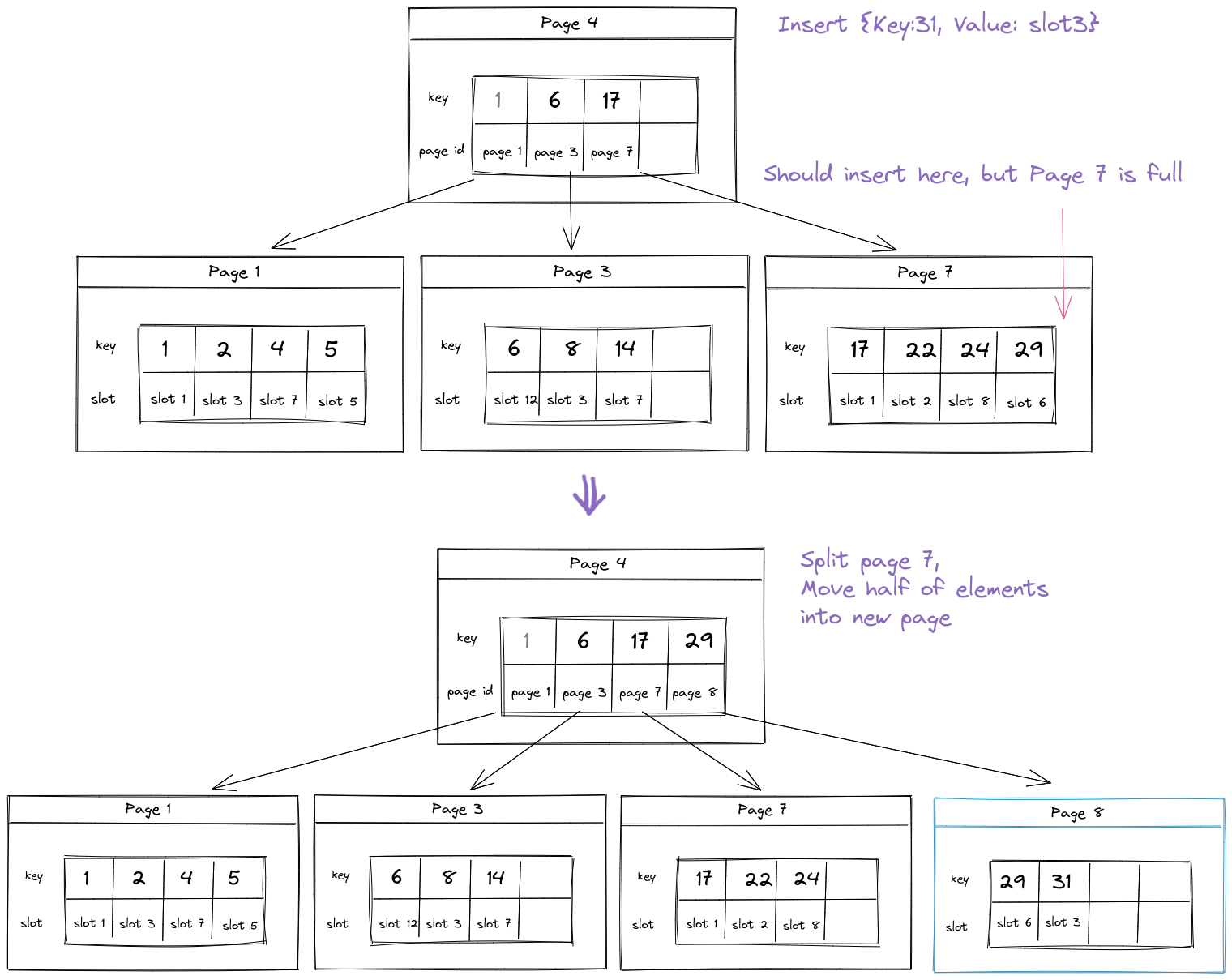
删除
删除操作需要考虑的情况比插入稍微多一点。假设中间节点的最多容纳 n 个指针,叶节点最多包含 n-1 个 k/v。
首先我们找到需要删除 k/v 所在的叶节点,如果
- 叶节点元素大于 $\lceil \frac{n-1}{2} \rceil$,那么可以直接删除而不用做其他调整;
- 叶节点元素等于 $\lceil \frac{n-1}{2} \rceil$,则删除该 k/v 之后我们需要对该叶节点与 sibling 进行调整保证叶节点元素不少于 $\lceil \frac{n-1}{2} \rceil$:
2.1 如果 node.size + sibling.size > LEAF_MAXSIZE=n-1,则需要将两个节点的元素重新分配,从元素更多的节点”借“一部分过来。注意这里的条件是两个节点的元素个数加起来大于 n-1,因此平均分配后每个节点的元素都能达到$\lceil \frac{n-1}{2} \rceil$ 个。另外 sibling 必须同属于一个 parent node(父母不同当然不能称为兄弟),不能简单通过叶节点的 next 指针取下一个叶子,如果右边的叶节点不是 sibling,那么要取左边的叶节点作为借元素的对象。由于父节点的元素个数总是大于2的,因此我们肯定能找到 sibling。
2.2 如果 node.size + sibling.size <= LEAF_MAXSIZE=n-1,此时无法通过 redistribute 使两个节点有 $\lceil \frac{n-1}{2} \rceil$ 个元素,因此需要合并 node 和 sibling。合并之后需要更新叶节点的 next 指针和 parent 指针,然后将被删除的叶节点从父节点的列表中删除。这导致父节点的元素也减少了,因此我们同样需要向上递归直到父节点元素大于$\lceil \frac{n-1}{2} \rceil$为止。
// TODO:merge // TODO:redistribute
B+ 树的更新操作基本就如上所示,虽然教材中伪代码加介绍用了七八页的篇幅,但是理解之后我们还是能用比较短的几段话概括出来的(大概还算短吧)。其实在实际编码过程中,插入和删除还算容易实现的,让人头疼的是我们下一篇要介绍的并发访问索引的情况,你将会看到如何使用 crabbing 算法提供更高的并发,同时保证正确性的。
To Be Continued…