一些笔记
先以纯01背包百练 2773的问题作为示例
首先是开辟二维dp数组的写法。dp[i][j]的含义为:i代表使用了[0~i]个物品计算的结果;j表示大小为j的背包能够装下的最大价值。所以对于物品[[71, 100], [69, 1], [1, 2]],要得到大小为70的背包能装下的最大价值,我们最后取dp[3][70]的值即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int main(){
int T = 0, M = 0;
cin >> T >> M;
vector<int> cost(M, 0), value(M, 0);
vector<vector<int>> dp(M, vector<int>(T + 1, 0));
for(int i = 0; i < M; i++) {
scanf("%d%d", &cost[i], &value[i]);
}
for(int i = cost[0]; i <= T; i++) {
dp[0][i] = value[0];
}
for(int i = 1; i < M; i++) {
for(int j = 1; j <= T; j++) {
if(cost[i] > j)
dp[i][j] = dp[i-1][j];
else
dp[i][j] = max(dp[i-1][j], dp[i-1][j - cost[i]] + value[i]);
}
}
cout << dp[M-1][T];
return 0;
}
把dp数组打印出来可能更好理解一些,下面是一个以cost:[2, 1, 4], value:[5, 4, 8], capacity:4的输入计算得到的二维数组。
首先初始化数组,可以在构建vector时全部初始化为0,然后单独初始化第一行
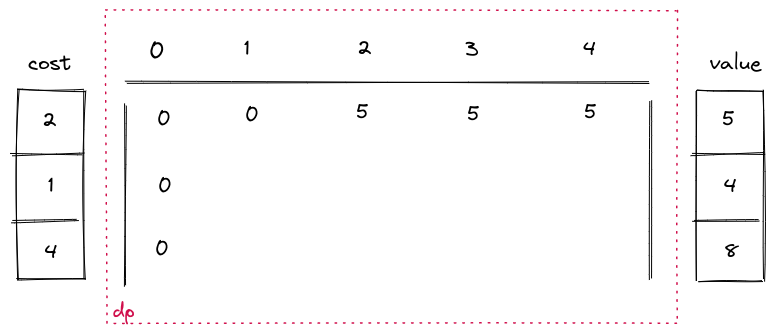
然后根据公式逐行计算

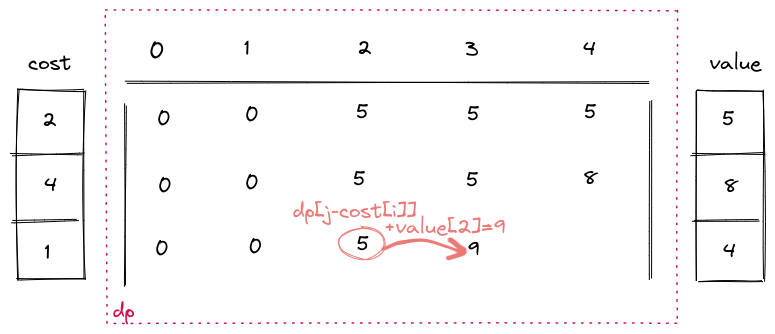
最终计算结果如下图
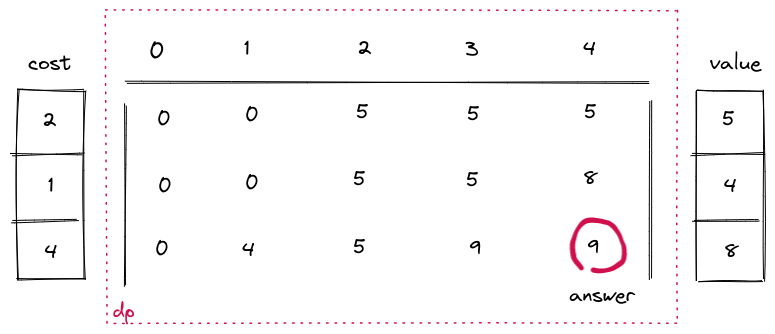
为了节省空间,也可以使用一维数组,类似的,dp[j]为容量j的背包能装下的最大值,外层循环每计算一次表示加入一个新的物品,dp[j - cost[i]] + value[i]项含义是 “计算前i个物品得到的容量为j-cost[i]背包的最大价值,加上取物品i,消耗cost[i]得到的价值value[i]后,背包装入的价值”。代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int main(){
int T = 0, M = 0;
cin >> T >> M;
vector<int> cost(M, 0), value(M, 0);
vector<int> dp(T + 1, 0);
for(int i = 0; i < M; i++){
scanf("%d%d", &cost[i], &value[i]);
}
for(int i = 0; i < M; i++){
for(int j = T; j >= cost[i]; j--){
dp[j] = max(dp[j], dp[j - cost[i]] + value[i]);
}
}
cout << dp[T];
return 0;
}
注意这里的内层循环要变成倒序。
note 1:采用一维数组时为何需要倒序。
背包九讲的解释是倒序访问时,数组中的 dp[j - cost[i]] 就相当与原本二维数组中的 dp[i-1][j - cost[i]];如果正序访问,因为 j 之前的元素在本次循环中已经更新了,相当与 dp[i][j - cost[i]],与二维版本不等价。 代码随想录中解释为如果正序访问,会造成元素被使用多次;倒序遍历时物品只放入了一次。
简单来说更新dp[i][j]需要的是dp[i-1][0…j]的部分,在二维数组中这部分元素肯定是保存着没有改变的,正序访问没什么问题;但是如果优化成一维之后,我们还按照正序计算,更新到dp[j+1]时,前面的dp[0…j]已经被计算过,相当与二维数组里的dp[i][0…j]了。所以我们要保证计算dp[j+1]时前面dp[0…j]对应二维数组上一行数据的话就需要倒序计算。
其实从另一个角度理解代码随想录的解释,正序计算相当于在解决完全背包问题。举个例子,假设j = 2时取物品3的总重量最大;而j=4时,j-cost[3] == 2,此时如果max(dp[j], dp[j - cost[i]] + value[i])取到的最大值是后者,那么表示 “在取了一次物品3的情况下,第二个物品还取物品3的价值最大”,即这里又取了一次物品3。所以说正序是在计算完全背包问题的解。
note 2:采用二维数组时,计算的双重循环顺序可以调换吗?一维数组时可以调换吗?为什么? 二维时可以,一维不可。
由于计算dp[i][j]时,我们只需要用到dp[0…i-1][j],也就是上一行的前j个元素(中的一部分),所以双重for循环内外层的顺序可以调换。改变上述
(TODO:画图解析
TODO:
note 3:(TODO)背包九讲关于01背包初始化的建议如何理解?
note 4:完全背包的内外循环可以调换吗,为什么?